OpenDSS Documentation

This section presents the technical details of implementation for the N Nodes Current Injection Method (NCIM) in OpenDSS, this algorithm was brought into OpenDSS for helping the simulator deal with transmission system-like simulation models.  NCIM is the latest version of the CIM algorithm originally developed by Martins et al [1], which later evolved into a three-phase equivalent (TCIM) [2] to finally fall into the area of multi-phase modeling [3]. This algorithm has been proposed for solving both, transmission and distribution, and given that the calculations are based on current injections similarly to the base power flow solution method in OpenDSS [4], NCIM represented the best alternative for complementing the needs of the simulator when solving transmission simulation models.

NCIM is a Newton-Raphson-based algorithm that models the system using a slack bus with other PQ and PV buses around. The conditions for the PQ buses are represented similarly to OpenDSS’ Floating point iterative (FPI) method, however, PV buses are different since the voltage and active power regulation differs from FPI by introducing the use of a decoupled-extended Jacobian matrix [5]. This method also allows to solve transmission systems using a multi-phase model formulation, compatible with OpenDSS providing a solution including zero sequence components if need it. This formulation differs from traditional positive sequence solvers and opens the door for extending the simulation capabilities for transmission systems into unbalanced cases.

The purpose of the example presented in this section is to serve as reference for future implementations and bug corrections.

Consider the circuit in Figure 3.

Figure 3. Test case proposed

 The circuit in Figure 3 includes 1 load (PQ bus) and 1 generator (PV bus), the generator connected to bus 3 will be the slack bus in this case. The technical settings for the load and generator are given in Table I.

Table I. technical features of the power conversion elements in the model

For the NCIM formulation the Y admittance matrix (YBUS) only considers the elements connected in series such as lines and transformers. Static shunt devices such as capacitors and reactors can be included in the YBUS. This is probably the main difference with FPI since it doesn’t consider Y primitives for PQ and PV buses in the YBUS matrix given that they are used for complementing the decoupled Jacobian. For this case, the YBUS matrix is as presented in Table II.

Table II. YBUS matrix for the circuit proposed

The NCIM algorithm is implemented as follows:

1. Calculate the YBUS matrix for the system.

2. Run a flat solution, this is, using:

Calculate the system initial voltages. The vector Inj will only have injecting currents at the slack bus, these currents are provided by the VSource element in OpenDSS. If you are in a different program, the initial voltage can be estimated as a flat start using the voltage bases of the buses. All the voltages are line to neutral. The reactive power for PV buses is equal to 0.

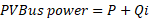
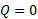
3. With the estimated V, calculate the current mismatches. First estimate the injection currents for the actual solution at the vector V. This solution is calculated as follows:

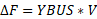
Reorganize the vector in its decoupled form, setting the imaginary part first and then the real part. As follows:

As a result, the vector ΔF will transform from a vector of complex into a vector of doubles.

Then, add the currents for the PQ and PV buses, for the PQ buses, the current injections will be added as:

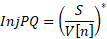
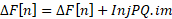
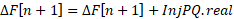
For the PV buses the injection current is calculated as:

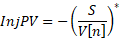
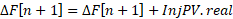
When including PV buses, the Jacobian matrix will include an extension for voltage and active power regulation as mentioned in [5], ending up in the following representation:

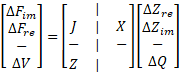
This representation suggests that the vector ΔF will be extended for including the voltage difference for the voltage regulation of the PV buses, which will serve as reference for calculating the reactive power injection/absorption required to reach the set point. Consequently, when calculating the current contribution of the PV bus it is also necessary to calculate the voltage difference ΔV using the following expression:

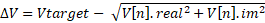
ΔV need to be added for each PV bus at the end of the vector ΔF aligning with each Z and X coefficient within the Jacobian matrix.

4. Evaluate the convergence criteria using vector ΔF. If the absolute value (|ΔF|) of all the elements in the vector are equal or below the convergence criteria, the solution has been found and go to step 12. Otherwise, go to step 5.

5. Calculate the Jacobian matrix, the elements of the Jacobian are based on the YBUS matrix in its decoupled form as explained in [1, 2], this is, the Jacobian matrix size is twice the size of the YBUS matrix plus the number of PV Buses multiplied by their number of phases. A cell of the Jacobian matrix based on a cell of the YBUS matrix will be represented as follows:

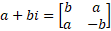
X and Z for the PV buses, is represented as indicated in [5].

6. Add the PQ bus coefficients to the Jacobian matrix. This only affects the diagonal of the Jacobian matrix and is calculated as follows:

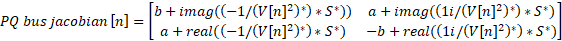
The a and b coefficients are the ones in the Jacobian matrix. Don’t use the ones from the YBUS, since there can be more loads or other elements connected to the same bus, requiring this value from the Jacobian. 

7. Add the PV bus coefficients to the Jacobian matrix. This only affects the diagonal of the Jacobian matrix and is calculated as follows:

The a and b coefficients are the ones in the Jacobian matrix. Don’t use the ones from the YBUS, since there can be more loads or other elements connected to the same bus, requiring this value from the Jacobian. 

8. Solve the Jacobian matrix as follows:

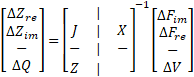
9. Add ΔZ to the voltage vector V, for that, transform vector ΔZ into its complex equivalent:

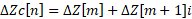
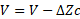
10. Update the reactive power for PV buses using the values obtained in ΔQ.

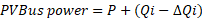
11. Go back to step 3.

12. Power flow solution found.